How Good is Our Model, Really?

Conceptual Overview

Purpose and Agenda

How do we interpret a machine learning model? What else can we say, besides how accurate a model this? This module is intended to help you to answer these questions by examining output from a classification and a regression model. We use a large data set, the Open University Learning Analytics Dataset (OULAD).

The key point to make here is that we will go well beyond the relatiely simplistic “Accuracy” metric, which is used to simply represent the proportion of the predictions that are correct. While useful, there are many other metrics that can give us a better sense of for which cases our SML model is making good predictions (e.g., just the “true” cases in a binary classification model, but not the “false” cases – or vice versa). You can make the point that this is especially important in our field, as different incorrect predictions may have different stakes (i.e., incorrectly classifying a student as needing additional support may not be directly harmful, but incorrectly predicting that a in fact student cheated may have substantial consequences). Metrics and interpreting them given the specifics of a particular analysis and context can help to avoid these harms, and to build the best performing models possible.

What we’ll do in this presentation

• Discussion 1
• Introducing the OULAD
• Key Concept #1: Accuracy
• Key Concept #2: Feature Engineering (part A)
• Key Concept #3: Metrics and their real-world interpretation
• Discussion 2
• Introduction to the other parts of this module

Make the point that we will engage much more deeply about feature engineering in the next module; we do this here to start the conversation and to open up some space in the next module for the complexity of cross-validation and a new type of model that we will use — a random forest.

Two notes

1. Sometimes, we do things that are a little bit harder in the short-term for pedagogical reasons (evaluating metrics with training data, for instance)—some of these frictions will go away when we progress to our “full” model (in the next module)
2. Whereas the last module was focused on a big concept (the importance of splitting data into training and testing sets), this module is focused on a bunch of concepts (different fit metrics) that are best understood when they are used in a variety of specific instances (when each metric is needed, used, and interpreted)

Discussion 1

• Background
• Getting Started
• Digging Deeper

• We are likely familiar with accuracy and maybe another measure, Cohen’s Kappa
• But, you may have heard of other means of determining how good a model is at making predictions: confusion matrices, specificity, sensitivity, recall, AUC-ROC, and others
• Broadly, these help us to understand for which cases and types of cases a model is predictively better than others in a finer-grained way than accuracy

• Think broadly and not formally (yet): What makes a prediction model a good one?

• After having worked through the first and second modules, have your thoughts on what data you might use for a machine learning study evolved? If so, in what ways? If not, please elaborate on your initial thoughts and plans.

This can connect back to the purpose at the beginning — try to elicit ideas that go beyond simple “Accuracy” to other, broader ideas about what makes a model good. These ideas can even extend beyond metrics (e.g., a learner may mention that the data is collected ethically) - these can be rich conversations to have here, but try to focus the conversation back on metrics as a nexus and tool for thinking about what makes an SML model a good one.

Introducing the OULAD

OULAD

• The Open University Learning Analytics Dataset (OULAD) is a publicly available dataset from the Open University in the UK
• It contains data on students enrolled in online courses, including their demographics, course interactions, and final grades
• Many students pass these courses, but not all do
• We have data on students’ initial characteristics and their interactions in the course
• If we could develop a good prediction model, we could provide additional supports to students–and maybe move the needle on some students succeeding who might not otherwise

OULAD files

We’ll be focusing on three files:

• studentInfo, courses, and studentRegistration

These are joined together (see oulad.R) for this module.

OULAD data

# A tibble: 3 × 15
  code_module code_presentation id_student gender region       highest_education
  <chr>       <chr>                  <dbl> <chr>  <chr>        <chr>            
1 AAA         2013J                  11391 M      East Anglia… HE Qualification 
2 AAA         2013J                  28400 F      Scotland     HE Qualification 
3 AAA         2013J                  30268 F      North Weste… A Level or Equiv…
# ℹ 9 more variables: imd_band <chr>, age_band <chr>,
#   num_of_prev_attempts <dbl>, studied_credits <dbl>, disability <chr>,
#   final_result <chr>, module_presentation_length <dbl>,
#   date_registration <dbl>, date_unregistration <dbl>

Key Concept #1

Accuracy

Let’s start with accuracy and a simple confusion matrix; what is the Accuracy?

Outcome	Prediction	Correct?
1	1	Yes
0	0	Yes
0	1	No
1	0	No
1	1	Yes

Accuracy Calculation

Use the tabyl() function (from {janitor} to calculate the accuracy in the code chunk below.

data_for_conf_mat %>% 
    mutate(correct = Outcome == Prediction) %>% 
    tabyl(correct)

 correct n percent
   FALSE 2     0.4
    TRUE 3     0.6

The limitation of accuracy

Model	Accuracy	Class_Distribution
Model A	0.8	85% Good, 15% Poor
Model B	0.7	15% Good, 85% Poor

Both models have 80% accuracy, but are they equally good?

This is central to the core purpose of this module - to get learners realizing the downsides of accuracy, given what accuracy can obfuscate.

Beyond accuracy: The need for nuance

• Accuracy is insufficient when:
  • Class distributions are imbalanced
  • Different types of errors have different consequences
  • You need to tune your model for specific objectives
• Example from OULAD data:
  • What if only 20% of students pass a class?
  • A model that always predicts “not pass” would have 80% accuracy, but is useless for identifying successful students
• We need metrics that tell us:
  • How well we identify positive cases (pass) and negative cases (fail)
  • How reliable our positive and negative predictions are

Confusion Matrix

Now, let’s create a confusion matrix based on this data - this lets us dive deeper into how good our models’ predictions are:

library(tidymodels)

data_for_conf_mat %>% 
    conf_mat(Outcome, Prediction)

          Truth
Prediction 0 1
         0 1 1
         1 1 2

Confusion Matrix Terms

Accuracy: Prop. of the sample that is true positive or true negative

True positive (TP): Prop. of the sample that is affected by a condition and correctly tested positive

True negative (TN): Prop. of the sample that is not affected by a condition and correctly tested negative

False positive (FP): Prop. of the sample that is not affected by a condition and incorrectly tested positive

False negative (FN): Prop. of the sample that is affected by a condition and incorrectly tested positive.

Confusion Matrix Visual

This and the next slide can take awhile to work through — it may be helpful to do some math on a whiteboard, and to ask lots of questions of learners to work through the math, which is simple mathematically but somewhat challenging conceptually! Take time here — this can be really valuable as a time and space to deeply understand what is under the hood of these metrics.

Metrics

Please note that Precision goes by the name Positive Predictive Value, whereas Negative Predictive Value does not have another commonly used name.

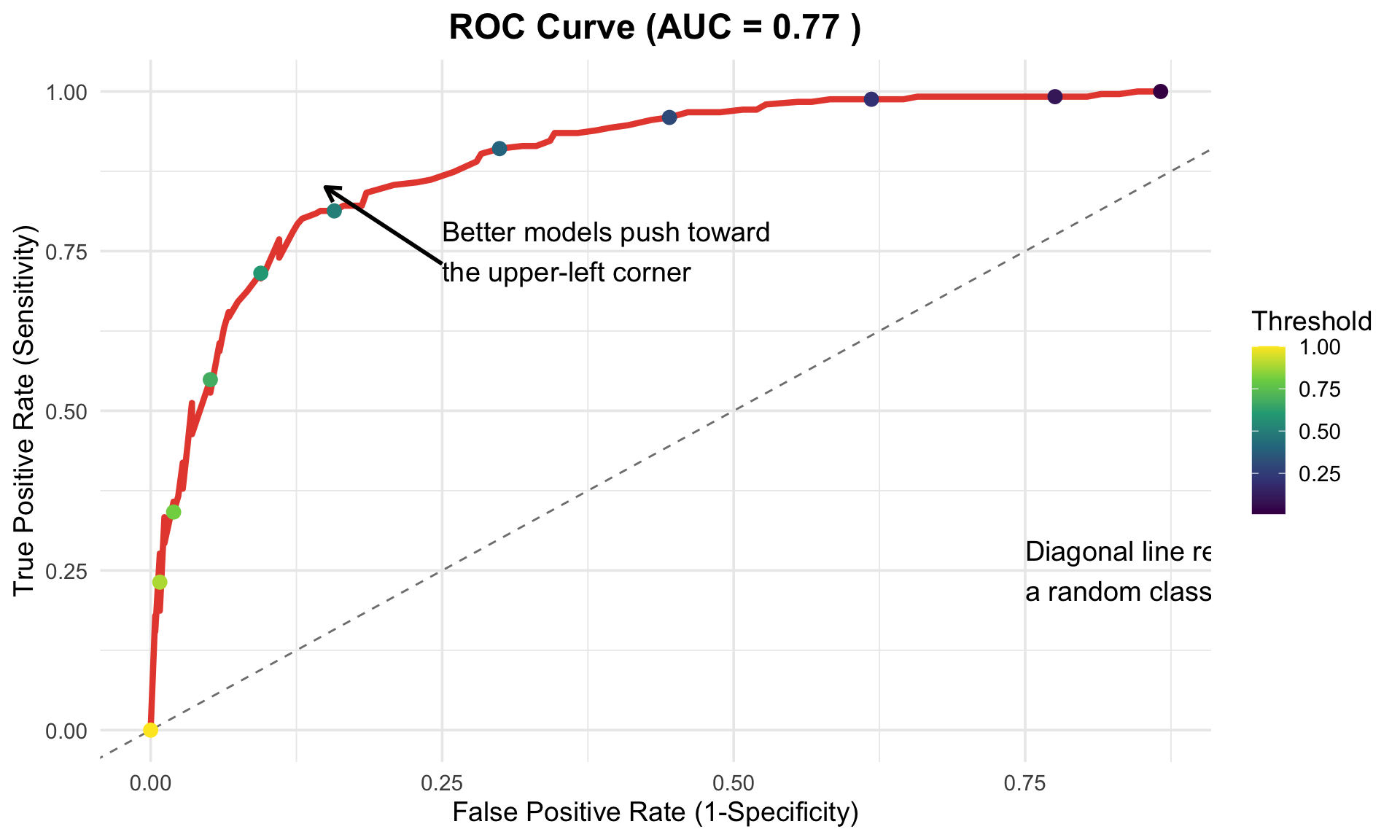
AUC-ROC

• Area Under the Curve - Receiver Operator Characteristic (AUC-ROC)
• Informs us as to how the True Positive rate changes given a different classification threshhold
• Classification threshhold: the probability above which a model makes a positive prediction
• Higher is better

Key Concept # 2

Feature Engineering (Part A)

Why?

Let’s consider a very simple data set, d, one with time_point data, var_a, for a single student. How do we add this to our model? Focus on the time element; how could you account for this?

d <- tibble(student_id = "janyia", time_point = 1:10, var_a = c(0.01, 0.32, 0.32, 0.34, 0.04, 0.54, 0.56, 0.75, 0.63, 0.78))
d %>% head(3)

# A tibble: 3 × 3
  student_id time_point var_a
  <chr>           <int> <dbl>
1 janyia              1  0.01
2 janyia              2  0.32
3 janyia              3  0.32

Why (again)?

How about a different variable, now focusing on the variable, var_b. How could we add this to a model?

d <- tibble(student_id = "janyia", time_point = 1:10, var_b = c(12, 10, 35, 3, 4, 54, 56, 75, 63, 78))
d %>% head(3)

# A tibble: 3 × 3
  student_id time_point var_b
  <chr>           <int> <dbl>
1 janyia              1    12
2 janyia              2    10
3 janyia              3    35

You can emphasize here that the interactions data is emblematic of much learning analyitcs data. You may want to open the data here to view it together, getting a sense of its size and contents in terms of rows (observations) and columns (variables).

What are some other ideas?

This can be a very fun discussion - lean into weird ideas! Writing these out on a whiteboard may help to facilitate sharing and discussion.

Other Options

A few (other) options

• Raw data points
• Their mean
• Their maximum
• Their variability (standard deviation)
• Their linear slope
• Their quadratic slope

You can lean into other ideas - writing other ideas (e.g., do moon phases matter for certain RQs!) on the whiteboard.

Each of these may derive from a single variable but may offer predictive utility as distinct features

Time Stamps

Here’s a time stamp:

[1] "2025-07-13 19:47:47 EDT"

How could this variable be used as a predictor variable?

How?

• We can do all of these things manually
• But, there are also helpful “{recipes}” functions to do this
• Any, the {recipes} package makes it practical to carry out feature engineering steps for not only single variables, but groups of variables (or all of the variables)
• Examples, all of which start with step():
  • step_dummy()
  • step_normalize()
  • step_inpute()
  • step_date()
  • step_holiday()

Emphasize this very brief introduction is to just begin to explore these topics (that we’ll explore in more depth in the next module), and to make our more sophisticated modeling possible

Key Concept #3: Metrics and their real-world interpretation

From confusion matrix to metrics

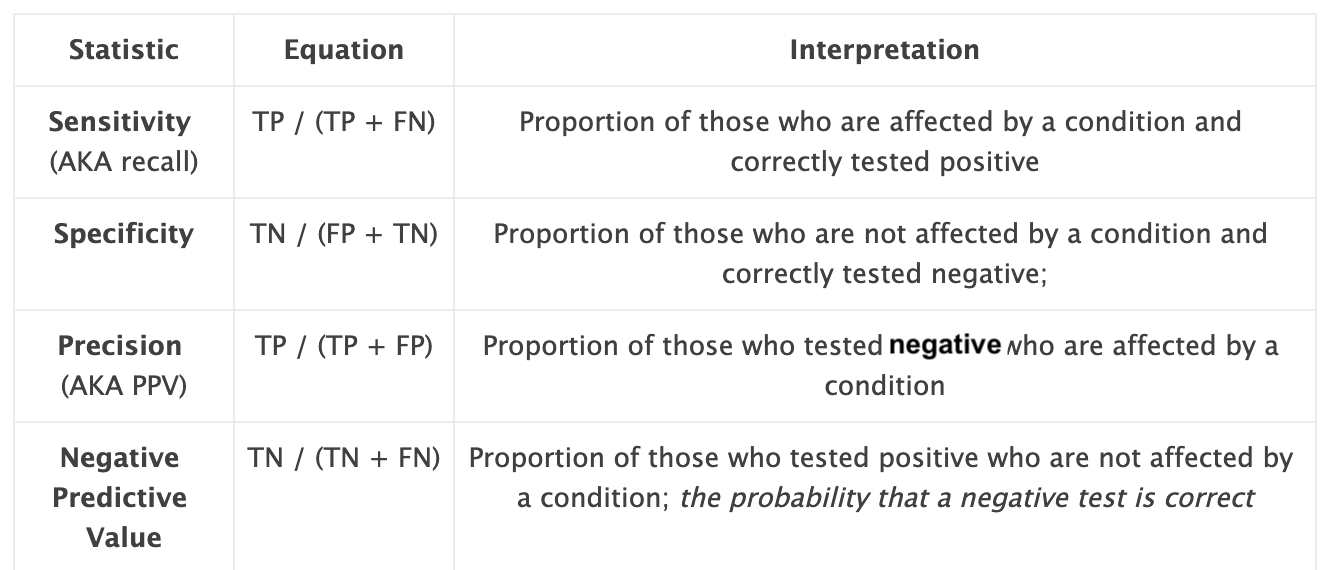
Metric	Formula	Question	Value
Accuracy	(TP + TN) / (TP + TN + FP + FN)	Overall, how often is the model correct?	80%
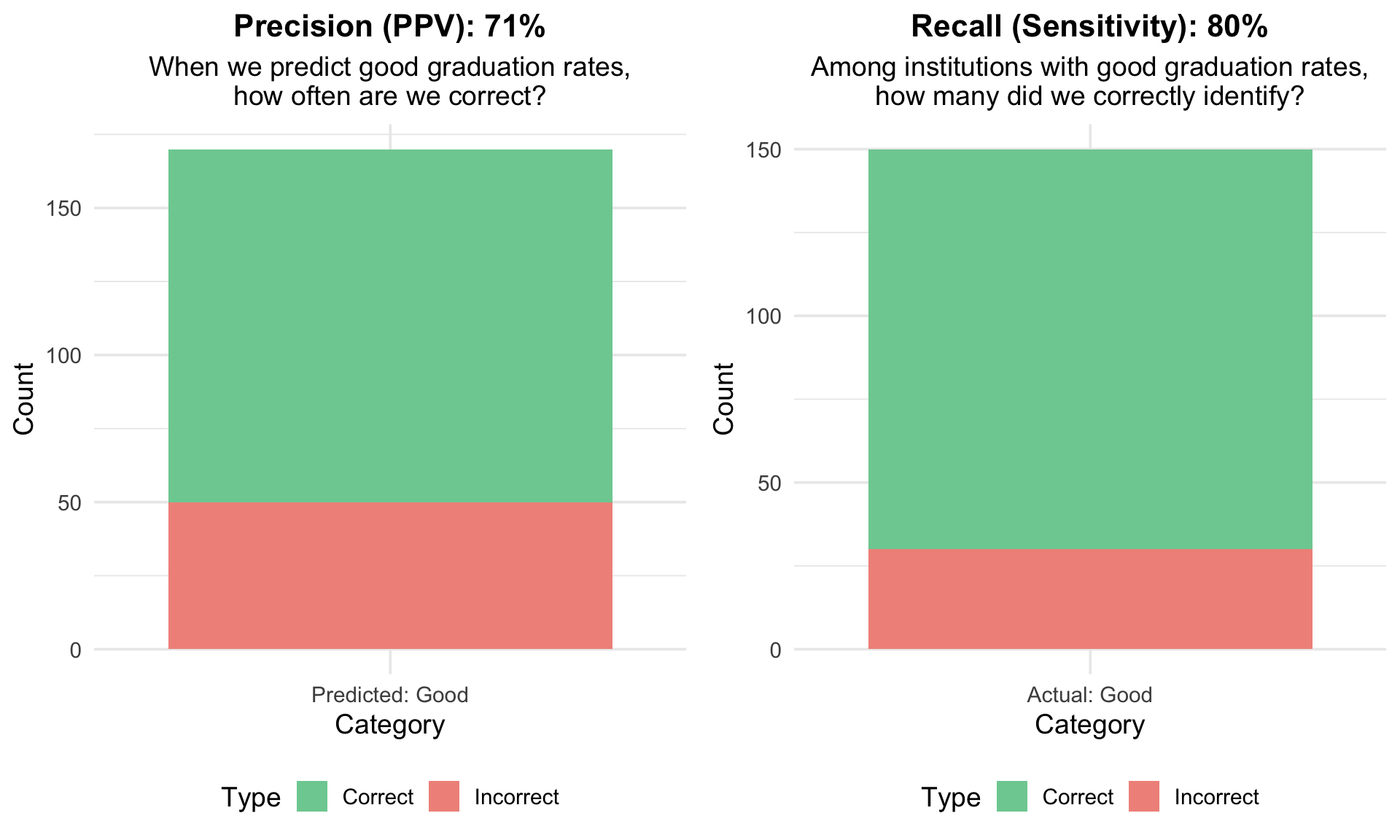
Sensitivity/Recall	TP / (TP + FN)	When an institution actually has good graduation rates, how often does the model predict this?	80%
Specificity	TN / (TN + FP)	When an institution actually has poor graduation rates, how often does the model predict this?	80%
Precision/PPV	TP / (TP + FP)	When the model predicts good graduation rates, how often is it correct?	71%
NPV	TN / (TN + FN)	When the model predicts poor graduation rates, how often is it correct?	87%
F1 Score	2 * (Precision * Recall) / (Precision + Recall)	What is the harmonic mean of precision and recall?	75%

Sensitivity vs. Specificity

Precision vs. Recall (Sensitivity)

F1 Score: The Harmonic Mean

What is F1 Score? - F1 = 2 × (Precision × Recall) / (Precision + Recall) - Harmonic mean balances precision and recall - Ranges from 0 to 1 (higher is better) - Only high when both precision and recall are high

Why harmonic mean instead of arithmetic mean? - Harmonic mean penalizes extreme values more severely - If either precision OR recall is very low, F1 will be low - Forces you to achieve balance between the two metrics

Emphasize that F1 score is particularly useful when you can’t decide whether precision or recall is more important, or when you need both to be reasonably high. The harmonic mean ensures that a model can’t “cheat” by excelling at one metric while ignoring the other.

When to Use F1 Score in OULAD Context

F1 Score is ideal when: - You need balanced performance on precision and recall - Both false positives AND false negatives are costly - You’re comparing multiple models and want a single metric - Class imbalance exists but you need to perform well on both classes

OULAD Example: - Scenario: Predicting students who need academic support - Goal: Find struggling students (high recall) while avoiding overwhelming support services (high precision) - F1 helps balance: Catching most at-risk students without flooding counselors with false alarms

Limitation: F1 score doesn’t tell you which metric is driving performance - you still need to examine precision and recall individually for full understanding

You can give a concrete example: “If your model has 90% precision but 40% recall, the F1 score will be about 55% - much lower than either individual metric. This forces you to improve the weaker metric rather than ignoring it.”

Metrics in Context: What Matters for OULAD?

When using the Open University Learning Analytics Dataset (OULAD) to build models that predict student outcomes at the module level (e.g., pass, fail, or withdrawal), the choice of which performance metrics to prioritize depends heavily on the specific goals of your analysis and the interventions or actions that will follow.

High Precision (Positive Predictive Value - PPV)

Is crucial if: * You aim to reliably identify students who are genuinely at high risk of failing or withdrawing, and interventions are costly or intensive. The focus is on minimizing false positives (wrongly labeling a student as at-risk when they are not). * You are allocating limited, high-impact support resources (e.g., one-on-one tutoring, intensive counseling) and want to ensure they reach students who truly need them. * The “cost” of a false positive is high (e.g., causing unnecessary anxiety for a student flagged as at-risk, or misdirecting scarce resources).

High Recall (Sensitivity)

Is crucial if: * Your primary goal is to identify as many students at risk of failing or withdrawing as possible, even if it means some students who would have ultimately passed are also flagged. The focus is on minimizing false negatives (failing to identify a student who will struggle). * You are implementing broad, lower-cost interventions (e.g., sending encouraging emails, pointing to general study resources, offering optional workshops) where wider reach is beneficial. * The “cost” of a false negative is high (e.g., missing the opportunity to support a student who subsequently fails or withdraws).

High Specificity

Is crucial if: * You want to accurately identify students who are not at risk and are likely to pass or achieve distinction, perhaps to study their successful learning patterns or to avoid unnecessary interventions. * You are trying to minimize the number of students incorrectly flagged for intervention who would have succeeded on their own (reducing “false alarms” for students not needing support). * Resources for “non-intervention” or “positive pathway” studies are limited, and you need to be sure you are focusing on genuinely low-risk students. :::

In Essence for OULAD:

• Prioritize Precision when targeted, resource-intensive interventions for at-risk students are planned.
• Prioritize Recall when broad, less costly interventions are available, and the main aim is to catch every potentially struggling student.
• Prioritize Specificity when the goal is to correctly identify students not needing intervention, or to study successful student cohorts with high confidence.

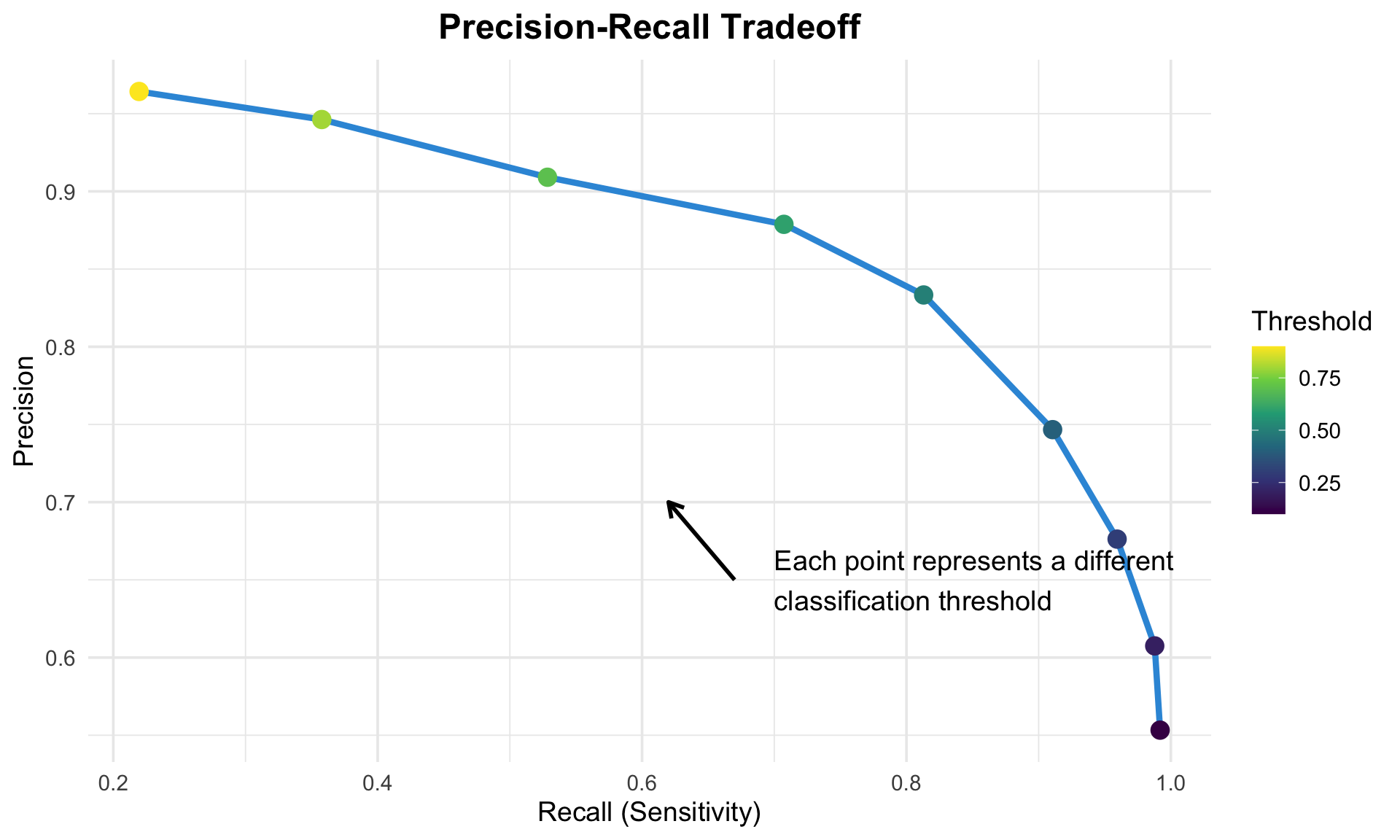
The precision-recall tradeoff

These next few slides get a little technical; may skip this, but it may be good to introduce this, too, and to return to later or engage in discussion based on students’ interests.

The ROC curve and AUC

Choosing the right classification threshold

The choice of threshold depends on your specific needs and priorities:

• Default threshold (0.5): Balanced, but often not optimal

• Lower threshold: Increases sensitivity, decreases specificity

  • Pro: Identifies more institutions with good graduation rates
  • Con: More false positives (incorrectly labeled as good)

• Higher threshold: Increases specificity, decreases sensitivity

  • Pro: More confident in positive predictions (high precision)
  • Con: Misses more institutions with good graduation rates

• Optimal threshold depends on:

  • The relative costs of false positives vs. false negatives
  • Available resources for intervention
  • Stakeholder priorities

Discussion 2

• Reflecting
• Applying

• Which metrics for supervised machine learning models (in classification “mode”) are important to interpret? Why?

• Thinking broadly about your research interest, what would you need to consider before using a supervised machine learning model? Consider not only model metrics but also the data collection process and how the predictions may be used.

Introduction to the other parts of this module

• Readings
• Case Study
• Badge

Baker, R. S., Berning, A. W., Gowda, S. M., Zhang, S., & Hawn, A. (2020). Predicting K-12 dropout. Journal of Education for Students Placed at Risk (JESPAR), 25(1), 28-54.

Baker, R. S., Bosch, N., Hutt, S., Zambrano, A. F., & Bowers, A. J. (2024). On fixing the right problems in predictive analytics: AUC is not the problem. arXiv preprint. https://arxiv.org/pdf/2404.06989

Maestrales, S., Zhai, X., Touitou, I., Baker, Q., Schneider, B., & Krajcik, J. (2021). Using machine learning to score multi-dimensional assessments of chemistry and physics. Journal of Science Education and Technology, 30(2), 239-254.

• Adding another data source from the OULAD, assessments data
• Interpreting each of the metrics in greater detail
• Using metric_set

• Stepping back and interpreting the model as a whole, focusing on moving beyond accuracy!
• Finding another relevant study

fin

General troubleshooting tips for R and RStudio