Module 1: Bayesian Knowledge Tracing

KT Learning Lab 1: A Conceptual Overview

A Little History

• The classic approach for measuring tightly defined skills in online learning

• First proposed by Richard Atkinson

• Most thoroughly articulated and studied by Albert Corbett and John Anderson Corbett and Anderson (1995)

Today, we will discuss Bayesian Knowledge Tracing, the classic approach for measuring tightly defined skills in online learning. It was first proposed, along with several other ideas, in a paper by Richard Atkinson in the ’60s, but it’s most associated with, most thoroughly articulated, and studied by Albert Corbett and John Anderson.

Flexibility of BKT

• Been around a long time

• Still as of today the most widely-used knowledge tracing algorithm used at scale

  • Interpretable

  • Predictable

  • Decent performance

Bayesian Knowledge Tracing has been around for a long time. It’s still the most widely used knowledge-tracing algorithm at scale because:

• It’s interpretable. 

• Its performance is very predictable, unlike some of the algorithms we’ll discuss later.

• Although its performance is as good as any of the modern alternatives, it still achieves good enough performance for many real-world tasks.

Goal & Assumptions

Transitioning slide, please move on

The Key Goal of BKT

• Measuring how well a student knows a specific skill/knowledge component at a specific time

• Based on their past history of performance with that skill/KC

The key goal of BKT is to:

• measure how well a student knows a specific skill or knowledge component at a specific time based on their past history of performance with that skill or K-C.

• The goal is not to measure overall skill for a broadly defined construct, such as arithmetic, but to measure a specific skill or knowledge component, such as adding two-digit numbers where no borrowing is needed

What is the typical use of BKT?

• Assess a student’s knowledge of skill/KC X

• Based on a sequence of items that are scored between 0 and 1

  • Classically 0 or 1, but there are variants that relax this

• Where each item corresponds to a single skill

• Where the student can learn on each item, due to help, feedback, scaffolding, etc.

The typical use of BKT is to: assess a student’s knowledge of a skill or knowledge component X. Based on the sequence of items that are dichotomously scored, the student can get a zero or a no on each item, with nothing in between. It turns out you can use BKT even for cases where there’s partial credit, but it’s not the most common use. Each item corresponds to a single skill. An item doesn’t have to be a separate problem; it could be a problem step and an overall problem that has a distinct skill associated with it. Students can learn about each item due to help, feedback, scaffolding, whatever. The point is that as the students practice, they are also learning.

Key assumptions of BKT

• Each item must involve a single latent trait or skill
  • Different from PFA, which we’ll talk about next lecture

• Each skill has four parameters

• Only the first attempt on each item matters

  • i.e. is included in calculations

• Help use usually treated as same as incorrect

  • Some exceptions I will discuss later

Key assumptions of Bayesian knowledge tracing:

• it assumes in its classical form that each item must involve just a single latent skill. Each skill has four parameters. Only the first attempt on each item matters, or in other words, is included in the calculations. 

• It’s also worth noting that help use is usually treated the same as incorrect. In other words, if the student asks for help, the system treats that as evidence that the student doesn’t know the skill. There are some exceptions to that in some variants on BKT, which I’ll discuss later.

Key assumptions of BKT Cont.

• Each skill has four parameters

• From these parameters, and the pattern of successes and failures the student has had on each relevant skill so far

• We can compute 

  • Latent knowledge P(L_n) 

  • The probability P(CORR) that the learner will get the item correct

From these parameters and the pattern of success and failures the student has had on each relevant skill so far, we can compute the student’s latent knowledge, P of Ln. How probable is the student to know the skill they are currently working on? 

We can also compute the probability P(CORR) that the learner will get the item correct.

Key assumptions of BKT

• Two-state learning model

• Each skill is either learned or unlearned

• In problem-solving, the student can learn a skill at each opportunity to apply the skill

• Each problem (opportunity) has the same chance of learning.

• A student does not forget a skill, once he or she knows it

Another key assumption is:

• a two-state learning model. Each skill is either learner, known, or unlearned, unknown. In problem-solving, the student can learn a skill and apply that skill at each opportunity. And a student doesn’t forget a skill once he or she knows it. 

• There are extensions of BKT that do allow for forgetting.

Model Performance Assumptions

• If the student knows a skill, there is still some chance the student will slip and make a mistake.

• If the student does not know a skill, there is still some chance the student will guess correctly.

The model also makes some performance assumptions:

• If a student knows a skill, there is still some chance that the student is going to slip and make a mistake. 

• At the same time, if the student doesn’t know the skill, there’s still some chance the student will guess and get the correct answer. So there’s a link between performance and learning, but it’s not a perfect link.

Comments or Questions?

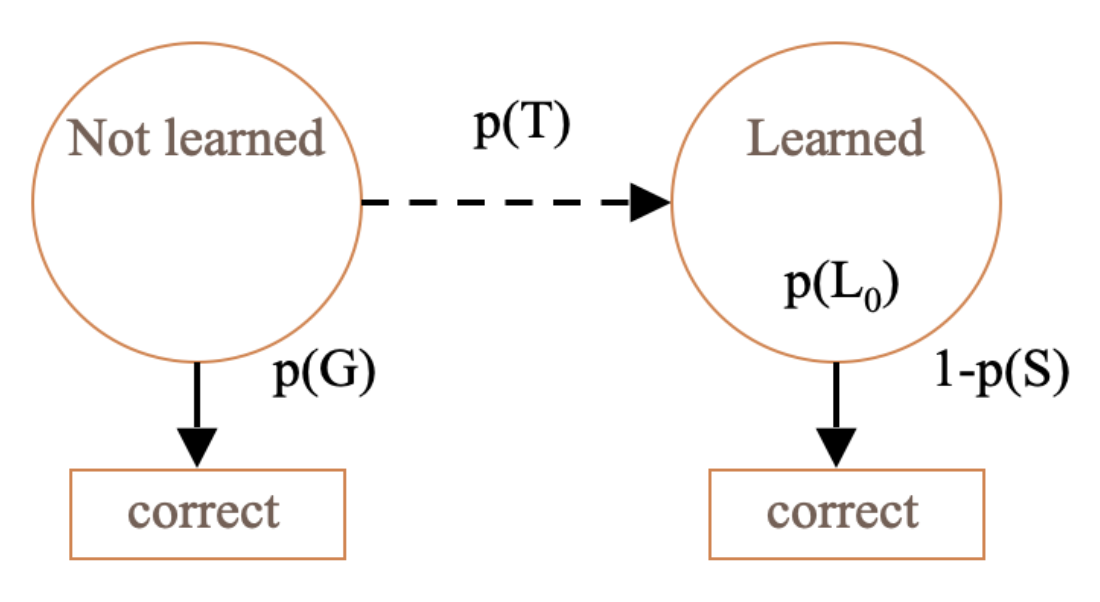
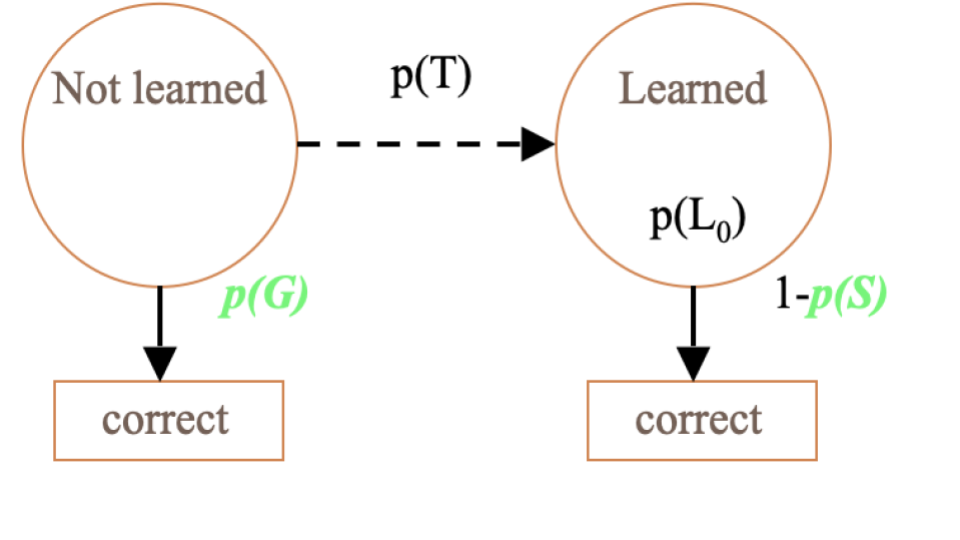
The BKT Model

Model Parameters & Predicting Correctness

Transition slide

Learning Parameters

Two Learning Parameters

1. p(L₀). Probability the skill is already known before the first opportunity to use the skill in problem solving.

2. p(T). Probability the skill will be learned at each opportunity to use the skill.

The first parameter, PL0, is the probability that the student already knows the skill before their first opportunity to use it in problem-solving. In other words, students don’t come into our learning system as a blank state. They come in already having a certain probability of knowing what we want them to know.

Learning Parameters

Two Learning Parameters

1. p(L₀). Probability the skill is already known before the first opportunity to use the skill in problem solving.

2. p(T). Probability the skill will be learned at each opportunity to use the skill.

Second, P of T is the probability that the skill will be learned at each opportunity to use it. If our system promotes learning at all, students’ performance should get better over time. They should actually learn, and P of T accounts for this.

Performance Parameters

Two Performance Parameters

1. p(G). Probability the student will guess correctly if the skill is not known.

2. p(S). Probability the student will slip (make a mistake) if the skill is known.

P of G, is the probability that the student will guess correctly if the skill is not known. So even if it’s not learned, even if they haven’t learned the skill, there is still a certain probability they will get it right.

Performance Parameters

Two Performance Parameters

1. p(G). Probability the student will guess correctly if the skill is not known.

2. p(S). Probability the student will slip (make a mistake) if the skill is known.

P of S, the probability that the student will slip and make a mistake even if the skill i known. Notice that the probability of current, given that you know it, is 1 minus P of S. In other words, if there’s a 20% chance that you’ll slip, then there’s an 80% chance you will get it right if you know it.

Comments? Questions?

Predicting Current Student Correctness

PCORR = P(L_n)P(S)+P(~L_n)P(G)

How do we predict current student correctness? 

• P-CORR is just the probability you know it, of LN, times the probability you didn’t slip, plus the probability you didn’t know it, times the probability you guessed. In other words, there are only two ways to get things correct in the world of Bayesian knowledge tracing. You know it and you don’t slip, or you don’t know it and you guess.

Bayesian Knowledge Tracing

• Whenever the student has an opportunity to use a skill

• The probability that the student knows the skill is updated 

• Using formulas derived from Bayes’ Theorem

  In Bayesian Knowledge Tracing, when the student has an opportunity to use a skill, the probability that the student knows the skill is updated using formulas derived from Bayes’ Theorem.

Formulas

\[ P(L_{n-1}|Correct_{n}) = \frac{P(L_{n-1})*(1-P(S))}{P(L_{n-1})*(1-P(S))+(1-P(L_{n-1}))*P(G)} \\\\\\ P(L_{n-1}|Incorrect_{n}) = \frac{P(L_{n-1})*(P(S))}{P(L_{n-1})*(P(S))+(1-P(L_{n-1}))*(1-P(G))} \\\\\\ P(L_{n}|Action_{n}) = P(L_{n-1}|Action_{n}) +(1- P(L_{n-1}|Action_{n}) * p(T)) \]

The formulas are as follows:

1. The probability that you knew it beforehand, given that you got it correct, is the probability that you knew it beforehand and didn’t slip over the probability you knew it and didn’t slip, plus the probability that you didn’t know it and you guessed.  

2. Similarly, if you got it wrong, then how did you get it wrong? You must have known it and slipped you already knew it. So if you already knew it, then you previously knew it and you slipped, and the two possibilities are you previously knew it and you slipped, and you didn’t know it and you didn’t guess.

3. Finally, once we know the probability that they knew it beforehand, given their correctness now, we can look at whether they learned it. So the probability that they know it at time n given action n, so after the action, is the probability they know it before the action, plus the probability they didn’t know it before the action, times the probability that they learned it. In other words, let’s say there’s a 30% chance you knew it after the previous action and a 10% chance you learned it. P of T is 10%. In that case, the probability you knew it afterward will be 0.3 plus 0.7, the probability you didn’t know it, times 0.1 for 0.37.

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
	0.4

Example:

If the probability they knew it beforehand is 0.4, the probability they learned it if they don’t know it is 0.1, the probability they slipped is 0.3, and the probability they guessed is 0.2. In that case, the initial probability they know it before they do anything in the system is 0.4. P of L zero becomes P of L n minus one. 

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	\[ \frac{(0.4)(0.3)}{(0.4)(0.3)+(0.6)(0.8)} \]
.
.
.

If they get it wrong. The probability they knew it beforehand is the probability they knew it beforehand without this information times the probability of being a slip because they got it wrong, over that probability plus the probability that they didn’t know it times the probability that they didn’t guess it. So 0.6 times 0.8. The inverse of 0.4 is 0.6,  and the inverse of 0.2 is 0.8.

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	\[ \frac{(0.12)}{(0.12)+(0.48)} \]
.

So when we compute that out, we get 0.2. (Please move on to the next slides)

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	0.2

Before we knew they got it wrong, we thought they had a 40% chance of knowing it. But after they get it wrong, we have a 20% chance that they know it. They still might have slipped.

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	0.2	0.2+(0.8)(0.1)

The probability that they know it afterward is the probability that they knew it plus the probability they didn’t know it times the probability they learned it.

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

 

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	0.2	0.28

And that is 0.28

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

 

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	0.2	0.28
	0.28

The probability that they know it afterward is the probability that they knew it before the second action.

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

 

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	0.2	0.28
1	0.28

If the student gets the action right.

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

  

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	0.2	0.28
1	0.28	\[ \frac{(0.28)(0.7)}{(0.28)(0.7)+(0.72)(0.2)} \]

If the student gets the action right. In that case, the probability they knew it before they got it right is the probability they had known it times hadn’t slipped. Over that probability, plus the probability that they didn’t know it and they guessed.

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

 

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	0.2	0.28
1	0.28	\[ \frac{(0.196)}{(0.196)+(0.144)} \]

Please move on to next slide

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	0.2	0.28
1	0.28	0.58

That turns into .58.

When they got it wrong, they went down from .4 to .2,  which came up to .28, and then that .28 after they got it right was reassessed to be .58. These are pretty big changes and that’s because the probabilities of slip and guess are pretty low on this model.

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

 

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	0.2	0.28
1	0.28	0.58	(0.58) + (0.42)(0.1)

So then the probability that they knew it afterward is the probability that they knew it beforehand, plus the probability that they didn’t know it times the probability they learned it,

Example

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

 

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	0.2	0.28
1	0.28	0.58	0.62

 which comes out to .62.

Your Turn

P(L₀) = 0.4, P(T) = 0.1, P(S) = 0.3, P(G) = 0.2

  

Actual	P(Ln-1)	P(Ln-1|actual)	P(Ln)
0	0.4	0.2	0.28
1	0.28	0.58	0.62
1

Comments? Questions?

Conceptual Idea Behind Knowledge Tracing

Parameter Constraints

• Typically, the potential values of BKT parameters are constrained

• To avoid model degeneracy

Typically the potential values of  BKT parameters are constrained.

The guess and slip we had are kind of low, so the model is fairly dynamic. However, we want to constrain those values somewhat to avoid what’s called model degeneracy, which is based on violating the conceptual idea behind knowledge tracing.

Conceptual Idea Behind Knowledge Tracing

• Knowing a skill generally leads to correct performance

• Correct performance implies that a student knows the relevant skill

• Hence, by looking at whether a student’s performance is correct, we can infer whether they know the skill

That conceptual idea is that knowing a skill generally leads to correct performance, and correct performance implies that a student knows the relevant skill. So, the idea is that by looking at whether a student’s performance is correct, we can infer whether they know the skill. 

Essentially

• A knowledge model is degenerate when it violates this idea

• When knowing a skill leads to worse performance

• When getting a skill wrong means you know it 

Essentially, a knowledge model is degenerate when it violates this idea. Knowing a skill leads to worse performance, and getting a skill wrong means that you know it. It’s weird, right? That’s why it’s called a degenerate model. Different people have proposed some constraints.

Parameter Constraints Proposed

• Beck

  • P(G)+P(S)<1.0

• R. S. d. Baker, Corbett, and Aleven (2008):

  • P(G)<0.5, P(S)<0.5

• Corbett and Anderson (1995)

  • P(G)<0.3, P(S)<0.1 

1. Joe Beck has proposed that the probability of guessing plus the probability of slip must be less than 1.

2.  Baker, Corbin, and Alavin have proposed that guess and slip each have to be less than 0.5.

3. Corbin and Anderson originally proposed, and this was not entirely just for model degeneracy but also based on some theorizing about what was probable, that P of G has to be less than 0.3 and P of S has to be less than 0.1.

4. Baker would say that when either guess or slip gets above 0.5,  you’re in a situation where the behavior doesn’t mean what it looks like.

5. Beck would say that for some cases where the modeling can get difficult, specifically like with automated speech responses where you’re making inferences, there might be enough error that you might get a guess or slip above 0.5. But as long as they’re under  1.0 as a sum, it’s still okay.

Knowledge Tracing

• How do we know if a knowledge tracing model is any good?

• Our primary goal is to predict knowledge

How do we know if a knowledge tracing model is any good beyond whether it is degenerate or not? The primary goal is to predict knowledge,

Knowledge Tracing

• How do we know if a knowledge tracing model is any good?

• Our primary goal is to predict knowledge

• But knowledge is a latent trait

• So we instead check our knowledge predictions by checking how well the model predicts performance

but knowledge is a latent trait. So, instead, we check our knowledge predictions by checking how all the models predict performance.

Fitting a Knowledge-Tracing Model

• In principle, any set of four parameters can be used by knowledge-tracing

• But parameters that predict student performance better are preferred

In principle, any set of four parameters can be used by knowledge tracing. However, parameters that predict student performance better are preferred.

Knowledge-Tracing

• So, we pick the knowledge tracing parameters that best predict performance

• Defined as whether a student’s action will be correct or wrong at a given time

So we try to pick the knowledge-tracing parameters that best predict performance. That is, whether a student’s action will be correct or wrong at a given time when knowledge tracing predicts it will be.

Are these the same thing?

• Predicting performance on next attempt

• Inferring latent knowledge

What are some alternate ways to assess

• Whether a model is successful at inferring latent knowledge

What are some alternate ways to assess

• Whether a model is successful at inferring latent knowledge

• Why aren’t those approaches used more often?

Comments? Questions?

Questions?

Fitting a Knowledge-Tracing Model

Fitting a Knowledge-Tracing Model

• In principle, any set of four parameters can be used by knowledge-tracing

• But parameters that predict student performance better are preferred

In principle, any set of four parameters can be used by knowledge-tracing.

But parameters that predict student performance better are preferred.

Fit Methods

I could spend an hour talking about the ways to fit Bayesian Knowledge Tracing models.

Three Public Tools

• hmmsclbl

  • https://pslcdatashop.web.cmu.edu/ExternalTools?toolId=1

• BNT-SM: Bayes Net Toolkit – Student Modeling

  • http://www.cs.cmu.edu/~listen/BNT-SM/

• BKT-BF: BKT-Brute Force (Grid Search)
  https://learninganalytics.upenn.edu/ryanbaker/BKT-BruteForce.zip

• Python Grid Search (slower than BKT-BF)

  • https://github.com/ChNabil/BKT_python_gridsearch

There are three public tools you can use to fit BKT parameters:

• HMMSCLBL by Michael Yudelson..

• BNT-SM, the Bayes Net Toolkit Student Modeling, which does expectation maximization

• BKTBF, BKT Brute  Force, which does a grid search algorithm.
  

All three of these are open on the web, and you can use them, they’re all fine really and work approximately equally well.

Which one should you use?

• They’re all fine – they work approximately equally well

• My group uses BKT-BF to fit Classical BKT and BNT-SM to fit variant models

• But some commercial colleagues use Fit BKT at Scale

All three of these are open on the web, and you can use them, they’re all fine really and work approximately equally well.

Note…

• The Equation Solver in Excel replicably does worse for this problem than these packages

The one thing you shouldn’t do is to use the Excel equation solver. That replicably does worse for the problem than these packages. So use some existing package - they’re out there.

How much data do you need? Slater and Baker (2018)

• Depends on your goal

• Predict student mastery, if ok to be off by 2-3 problems: 

  • As few as 25 students and 3 problems apiece, if P(T) values are low

•  Predict student mastery, if higher precision desired:

  • 250 students and 3 problems apiece

• Make inferences about model parameter values (for example, to identify skills that need to be fixed)

  • 250 students and 6 problems apiece

One common practical question that people ask is:

• how much data you need to fit BKT. 

• The answer depends on your goal. As Slater and Baker’s large-scale simulation study showed, if you’re intending to predict student mastery, and it’s ok for the system to decide the student has mastered two or three problems too early or too late, you can get away with as few as 25 students and 3 problems per skill, as long as P(T) values are low. If you do this, and see high P(T) values, you might need to get more data. If you want high precision on exactly when the student mastered, you might want to go as high as 250 students, but 3 problems per student is still generally OK. A harder task is making inferences about model parameter values. You might do this if, for example, you want to find skills with really high slip or guess rates, to fix them. In this case, you need 250 students and 6 problems per student.

BKT: Core Uses

• Mastery learning

• Reports to teachers on student skill

The two core uses of BKT are, of course:

1. supporting mastery learning – determining when a student has mastered a skill in order to advance them

2. and providing reports to teachers (or the student themself) on what skills the student has and hasn’t yet mastered.

BKT: Extended Uses

• Use in behavior detectors (such as gaming the system)

• Use to identify problematic skills for re-design (with very high slip or guess or initial knowledge)

• Use in discovery with models analyses (such as correlating student in-platform learning to test scores)

But there are several other common uses as well, including using BKT estimates as components in behavior detectors, like gaming the system, or identifying skills with very high slip or guess or initial knowledge, to drive iterative improvement of the learning system, or in variables in various kinds of analyses, like correlation students’ performance and learning within a learning platform, to external measures like their test scores.

BKT: Extended Uses

• Conditionalizing P(T) 

  • Does help help? (Beck et al. (2008))

  • Which content is most effective? (Ryan S. Baker, Gowda, and Salamin (2018))

There have been a bunch of extensions to BKT. It’s not just a good model, it’s also been the basis for a lot of other interesting work.

BKT: Extended Uses

• Moment-by-moment learning estimation
  (calculating P(T) in specific step)

• Which moment-by-moment learning curves are associated with more robust learning? (Ryan S. Baker et al. (2013))

• What behaviors predict “eureka” moments (Moore, Baker, and Gowda (2015))

• Which types of content are associated with more learning? (Slater et al. (2016))

Some examples here, they will be introduced later in Advanced BKT part.

BKT: Extended Uses

• Detecting carelessness (contextual slip)
  (calculating P(S) in specific step)

• Predicts test score (Pardos et al. (2014)), college enrollment (M. O. Pedro et al. (2013)), job several years later (Almeda and Baker (2020))

Some examples here, they will be introduced later in Advanced BKT part.BKT: Extended Uses

BKT: Extended Uses

• Transfer assessment
  (adding P(T) from other skills)

• Used to study relationship between skills (M. S. Pedro et al. (2014))

• Including in graduate students learning research skills across several years (Kang et al. (2022))

Some examples here, they will be introduced later in Advanced BKT part.BKT: Extended Uses

Further Discussion

How can you apply these methods to your own research or practice?

DISCUSSION: 

• How can you apply these methods to your own research or practice?

What’s NEXT?

• Complete the ASSISTments activity: [insert link here]

• Complete the badge requirement document: [insert link here]

Thank you! Any questions?

What’s next?

• assignments

More Detail on Advanced BKT

More Detail on Advanced BKT

• BKT has strong assumptions

• One of the key assumptions is that parameters vary by skill, but are constant for all other factors

• What happens if we remove this assumption?

Modifying the assumptions of Bayesian knowledge tracing:

• BKTS has strong assumptions. One key assumption is that parameters vary by skill but are constant for all other factors. What happens if we remove this assumption?

BKT with modified assumptions

• Conditionalizing Help or Learning

• Contextual Guess and Slip

• Moment by Moment Learning

• Modeling Transfer Between Skills

If we remove any of those assumptions, we get different kinds of algorithms that can be used for different purposes, like algorithms for conditionalizing help or learning, algorithms for contextual guess and slip, moment-by-moment learning models, and algorithms that can model the transfer between skills.

Beck, Chang, Mostow, & Corbett 2008

• Beck, J.E., Chang, K-m., Mostow, J., Corbett, A. (2008) Does Help Help? Introducing the Bayesian Evaluation and Assessment Methodology. Proceedings of the International Conference on Intelligent Tutoring Systems.

Now let’s first discuss Beck’s help model.

Notes

• In this model, help use is not treated as direct evidence of not knowing the skill

• Instead, it is used to choose between parameters

• Makes two variants of each parameter

  • One assuming help was requested 

  • One assuming that help was not requested

In this model, help use is not treated as direct evidence of not knowing the skill,  unlike classical BKT, but instead, it’s used to choose between parameters. This model makes two variants of each parameter, one of them assuming help was requested and one of them assuming that help was not requested.

Beck, et al.’s (2008) Help Model

This model otherwise looks just like BKT, at every single parameter,  there are two variants of it, a given help, a given H, and a given not help, given not H. This gives us eight parameters per skill: the four classical parameters times two.

Beck, et al.’s (2008) Help Model

• Parameters per skill: 8

• Fit using Expectation Maximization

-   Takes too long to fit using Grid Search

It fits using expectation maximization because it takes too long to fit using brute force. Brute Force works when we’ve got an N to the fourth problem, but it doesn’t work so well for an N to the eighth problem.

Beck, et al.’s (2008) Help Model

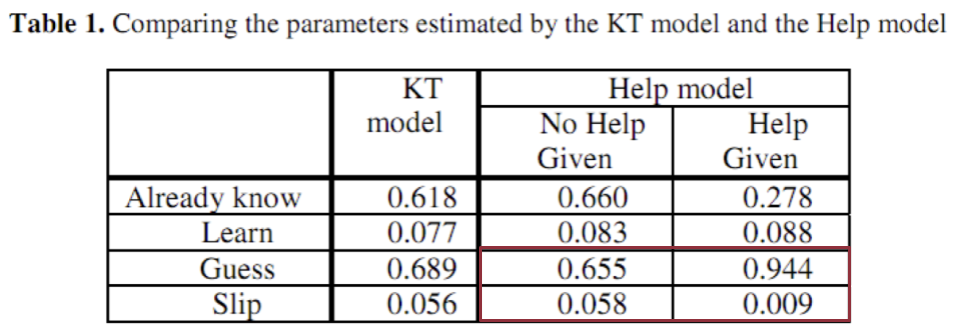
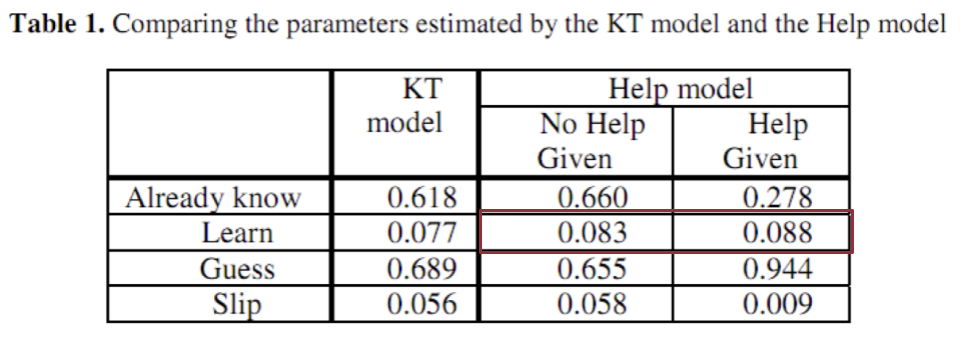
In his original paper, he found that there were fairly different parameter values for guess and slip based on whether or not the person asked for help.

Beck, et al.’s (2008) Help Model

(Explaining about the difference)

Notes

• This model did not lead to better prediction of student performance

• But useful for understanding effects of help

It’s worth noting that:

•  this model didn’t lead to a better prediction of student performance, but it was useful for understanding the effects of help. One thing about BKT that’s noteworthy is that a lot of the modern extensions of BKT actually aren’t about fitting the data better.

• A lot of the things that BKT can do for you have to do not with getting slightly better prediction of next problem correctness,  but with being able to infer other things.

BKT with modified assumptions

• Conditionalizing Help or Learning

• Contextual Guess and Slip

• Moment by Moment Learning

• Modeling Transfer Between Skills

The 2nd modification of assumptions of BKT is contextual guess and slope.

Contexual Guess-and-Slip

• Baker, R.S.J.d., Corbett, A.T., Aleven, V. (2008) More Accurate Student Modeling Through Contextual Estimation of Slip and Guess Probabilities in Bayesian Knowledge Tracing. Proceedings of the 9th International Conference on Intelligent Tutoring Systems, 406-415.

The 2nd modification of assumptions of BKT is contextual guess and slipe.

Contexual Guess-and-Slip

In this model, we have the exact same L0, T, G, and S, but the G and S aren’t parameters per skill. They’re models.

Contexual Slip: The Big Data

• Why one parameter for slip

  • For all situations

-   For each skill

• When we can have a different prediction for slip

  • For each situation

  • Across all skills

The big idea is why one parameter for slip for all situations for each skill when we can have a different prediction for slip for each situation across all skills.

In other words

• P(S) varies according to context 

• For example

  • Perhaps very quick actions are more likely to be slips

  • Perhaps errors on actions which you’ve gotten right several times in a row are more likely to be slips

In other words, P of S  varies according to context.

• Example: perhaps very quick actions are more likely to be slips, or perhaps errors in actions that you’ve gotten right several times in a row are more likely to be slips.

Contexual Guess and Slip Model

• Guess and slip fit using contextual models across all skills

• Parameters per skill: 2 + (P (S) model size)/skills + (P (G) model size)/skills

Guess and slip are therefore fit using contextual models across all skills.

In this case, the parameters per skill are 2 plus the model size of P  of S divided by the number of skills plus the guess model size divided by skills. This ends up amortizing to a good bit less than four parameters per skill.

How are these models developed?

1. Take an existing skill model 

2. Label a set of actions with the probability that each action is a guess or slip, using data about the future

3. Use these labels to machine-learn models that can predict the probability that an action is a guess or slip, without using data about the future

4. Use these machine-learned models to compute the probability that an action is a guess or slip, in knowledge tracing 

How are these models developed? 

• We take an existing skill model, and label a set of actions with the probability that each action is a guess or a slip using data about the future. We’re going to use the data about the future,  but we’re not actually going to use it in the running model.

• We use these labels to machine learning models that can predict the probability that an action is a guess or a slip without using data about the future.

• We then use these machine learning models to compute the probability that an action is a guess or a slip in real-time knowledge tracing.

Again, we’re using the future to build the models, but we’re not using the future to actually run the models.

How are these models developed?

2. Label a set of actions with the probability that each action is a guess or slip, using data about the future

• Predict whether action at time N is guess/slip

• Using data about actions at time N+1, N+2

• This is only for labeling data! @

• Not for use in the guess/slip models

More specifically, we label a set of actions with the probability that each action is a guess or a slip using data about the future. Predict whether an action at a time is a guess or a slip using data about the actions at time n plus 1 and n plus 2.

How are these models developed?

2. Label a set of actions with the probability that each action is a guess or slip, using data about the future

• The intuition:

• If action N is right

• And actions N+1, N+2 are also right

  • It’s unlikely that action N was a guess

• If actions N+1, N+2 were wrong

  • It becomes more likely that action N was a guess

• I’ll give an example of this math in few minutes…

The intuition is that if action n is right and actions n plus 1 and n plus 2 were also right, it’s probabilistically unlikely that action n was a guess because the probability that you’d get three things right in a row by guessing is just really infinitesimal. Similarly, if actions n plus 1 and n plus 2 were wrong, it becomes more likely that action n was a guess.

How are these models developed?

3. Use these labels to machine-learn models that can predict the probability that an action is a guess or slip

• Features distilled from logs of student interactions with tutor software

• Broadly capture behavior indicative of learning

  • Selected from same initial set of features previously used in detectors of 

    • gaming the system (R. S. d. Baker et al. (2008))

    • off-task behavior (R. Sj. Baker (2007))

Having gotten these labels, we then use them to machine-learn models that can predict the probability that an action is a guess or a slip. We take features distilled from logs of student interactions of the tutor software that broadly capture behavior indicative of learning.

• Baker-Corbinolev 2008,  it selected these from the same set of initial features previously used in detectors of gaming a system and off-task behavior.

How are these models developed?

3. Use these labels to machine-learn models that can predict the probability that an action is a guess or slip

• Linear regression

  1. Did better on cross-validation than fancier algorithms

• One guess model

• One slip model

In the first work, we used linear regression, which, in this early work, did better on cross-validation than fancier algorithms. One guess model, one slip model.

How are these models developed?

4. Use these machine-learned models to compute the probability that an action is a guess or slip, in knowledge tracing

• Within Bayesian Knowledge Tracing

• Exact same formulas

• Just substitute a contextual prediction about guessing and slipping for the prediction-for-each-skill

Having these probabilities, we just plug the estimates, the numbers, into Bayesian knowledge tracing,  the exact same formulas as before. We’re just substituting a contextual prediction about guessing and slipping for the prediction for each skill.

BKT with modified assumptions

• Conditionalizing Help or Learning

• Contextual Guess and Slip

• Moment by Moment Learning

• Modeling Transfer Between Skills

A third way to modify BKT’s assumptions: 

• moment-by-moment learning.

Moment-by-Moment Learning Model

Baker, R.S.J.d., Goldstein, A.B., Heffernan, N.T. (2011) Detecting Learning Moment-by-Moment. International Journal of Artificial Intelligence in Education, 21 (1-2), 5-25.

A third way to modify BKT’s assumptions: 

• moment-by-moment learning.

Moment-by-Moment Learning Model (Baker, Goldstein, & Heffernan, 2010)

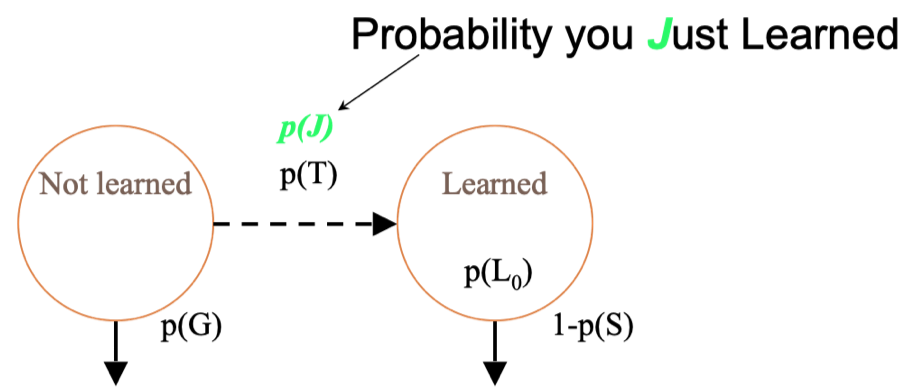
The moment-by-moment learning model, as published, uses Bayesian knowledge tracing and doesn’t try to substitute any of the four parameters. It just adds a variant parameter for P  of T, the probability you just learned. That’s not quite the same as P of T.

P(J)

• P(T) = chance you will learn if you didn’t know it

• P(J) = probability you Just Learned

  • P(J) = P(~L_n ^ T)

P of T is the chance you’re going to learn if you didn’t know it already. P of J is the probability you just learned. In other words, it’s the probability that you didn’t know it and then you learned it. Not quite the same thing,  although it’s quite related.

P(J) is distinct from P(T)

When say P of J is distinct from P of T, they can have values that are quite different.

• Example: the difference between a probability of T of 0.6 in the context where you have an initial probability of knowing it of 0.1 or 0.96. If you had a 10% chance of knowing it and you have a 60% chance of learning it if you didn’t know it, the probability you just learned is 54%.

• That’s a lot of learning

• That’s learning. But if your probability of knowing it to begin with was 96% and you had a 60% chance of learning it, you only have a 2% chance that you just learned it. That’s not very much learning.

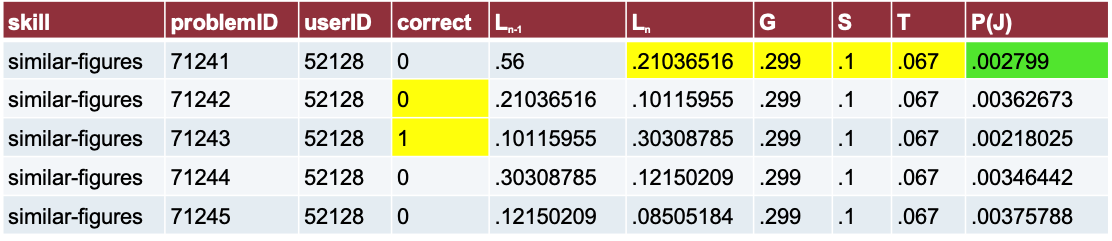
Labeling P(J)

• Based on this concept:

  • “The probability a student did not know a skill but then learns it by doing the current problem, given their performance on the next two.”

P(J) = P(~Ln ^ T | A+1+2 )

*For full list of equations, see
Ryan SJD Baker, Goldstein, and Heffernan (2011)

P of J is labeled based on the concept. It’s very similar to the contextual guess and slip model. The probability a student doesn’t know a skill but then learns it by doing the current problem given their performance on the next two.

Breaking down  P(~L_n ^ T | A+1+2 )

We can calculate the probability that they didn’t know it and they learned it from those next two actions with an application of Bayes’ theorem. We say the probability they didn’t know it and learned it given the next two actions is the probability of those next two actions given that they didn’t know it and they learned it times the probability that in general, regardless of those two actions, they didn’t know it and they learned it over the probability of those next two actions across all contexts.

Breaking down P(A+1+2 | L_n) P(L_n): One example

P(A+1+2 = C, C | Ln ) = P(~S)P(~S)

P(A+1+2 = C, ~C | Ln ) = P(~S)P(S)

P(A+1+2 = ~C, C | Ln ) = P(S)P(~S)

P(A+1+2 = ~C, ~C | Ln ) = P(S)P(S)

Example:

• What about the probabilities of the next two actions, given that they knew it, times the probability that they knew it? Well, there are only 4 possibilities for those two actions.

  • Correct, correct.

  • Correct, not correct.

  • Not correct, correct.

  • And not correct, not correct.

And those turn out to be if you knew it, the probability of correct, correct if you knew it is the probability you didn’t slip,  times the probability you didn’t slip.

The probability that you got it wrong and then right if you knew it was the probability you didn’t slip, times the probability you slipped, and so on.

This case is going to be more complicated for the case that you didn’t know it and you didn’t learn it because in that case, we’re trying to estimate the probability as we go forward based on the possibility that you may have learned it or not between the first and second attempts. So, the equations get really complicated at this point.

Features of P(J)

• Distilled from logs of student interactions with tutor software

• Broadly capture behavior indicative of learning

  • Selected from same initial set of features previously used in detectors of 

    • gaming the system (R. S. d. Baker et al. (2008))

    • off-task behavior (R. Sj. Baker (2007))

    • carelessness (R. S. d. Baker, Corbett, and Aleven (2008))

Now P of J, like contextual P of S and G, we took features distilled from logs of student interactions with tutor software that broadly captured behaviors indicative of learning. These features were selected from the same initial set of features previously used in detectors of gaming the system, off-task behavior, and carelessness, aka the probability of contextual slip.

Features of P(J)

• All features use only first response data

• Later extension to include subsequent responses only increased model correlation very slightly – not significantly

All the features in the original work used only first response data. Later extensions to include subsequent responses only increased the model correlation very slightly, not statistically significantly.

Uses

• Patterns in P(J) over time can be used to predict whether a student will be prepared for future learning (Hershkovitz et al. (2013), Ryan S. Baker et al. (2013)) and standardized exam scores (Jiang et al. (2015))

• P(J) can be used as a proxy for Eureka moments in Cognitive Science research (Moore, Baker, and Gowda (2015))

We then had a model that we could use for a few things.

• We’re not using this model at any point to try to improve our prediction of student performance in the system. Instead, we’re looking at how we can use this in analysis. It turns out that patterns in P of J over time can be used to predict whether theit’s student is prepared for future learning:.

• when they encounter the first piece of curriculum material beyond this current system can they actually learn from it and do well on a test. Patterns of P of J during the use of the system turn out to be predictive of this. Also, it turns out that P of J over time can be used to predict standard as exam scores.

• in a third recent use, P of J can be used as a proxy for eureka moments in cognitive science research. We can look for moments where students had spectacularly high learning, say higher than 99 percent of all learning episodes, and say what distinguishes the behavior that precedes this.

Alternate Method

• Assume at most one moment of learning

• Try to infer when that single moment occurred, across entire sequence of student behavior

  De Sande (2013) Pardos and Yudelson (2013)

• Some good theoretical arguments for this – more closely matches assumptions of BKT

• Has not yet been studied whether this approach has same predictive power as P(~Ln ^ T | A+1+2 ) method

There is an alternate method for calculating P of J:

we assume at most one moment of learning, and then we try to infer when that single moment occurred across the entire sequence of student behavior. This was done both by Van de Sande (2013) and by Pardos & Yudelson (2013). There are some good theoretical reasons why you might want to do this. It actually more closely matches the assumptions of BKT.

Is it better? We don’t know yet. 

Although there have been a couple of papers on it, we haven’t yet seen anyone study whether this approach has the same predictive power as the method from Baker-Goldstein-Heffernan for things like predicting preparation for future learning. Stairway as the exam scores or Eureka moments.

BKT with modified assumptions

• Conditionalizing Help or Learning

• Contextual Guess and Slip

• Moment by Moment Learning

• Modeling Transfer Between Skills

A fourth type of modifying the assumption of  BKT is modeling transfer between skills.

• This is unlike the other three, for which we’re still looking within a skill essentially, even though some of the variants in contextual guessing slip vary by skill.

• This one actually says what if we relax the assumption that each skill is independent from every other skill?

Modeling Transfer Between Skills

Sao Pedro, M., Jiang, Y., Paquette, L., Baker, R.S., Gobert, J. (2014) Identifying Transfer of Inquiry Skills across Physical Science Simulations using Educational Data Mining. Proceedings of the 11th International Conference of the Learning Sciences.

The first paper on this comes from Sao Pedro and colleagues in 2014, and what this model did was it said as follows:

How this model works

• Classic BKT: Separate BKT model for each skill

• BKT-PST (Partial Skill Transfer) M. S. Pedro et al. (2014): Each skill’s model can transfer in information from other skills

  1. BKT-PST: One time (when switching skill)

  2. BKT-PSTC Kang et al. (2022): At each time step

Classic BKT said says that there would will be a separate BKT model for each skill. BKT-PST partial skill transfer says instead that each skill model can transfer information from other skills, and in its original formulation in 2014, this happened exactly once when switching between skills in a system. But in Kang et al., in 2022 said wait a minute sometimes you switch back and forth between skills. So in that case we’re going to do it at each time step.

BKT-PST/PSTC Model

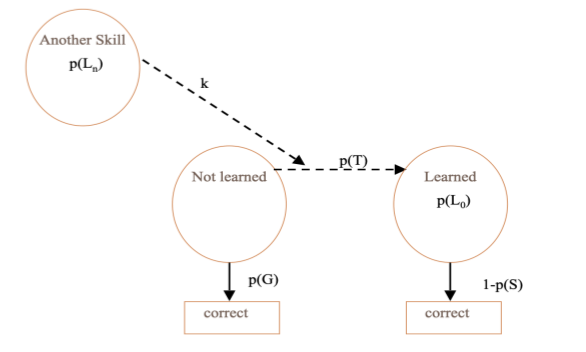
The BKT PST or PSTC model is basically the original BKT graph, which you see at the bottom. But then from some other skill, there’s a transfer in which has parameter K. This method of transferring information between skills hasn’t been used a ton but it has been used by Sale Pedro and colleagues to study the relationship between skills in a science simulation.

Uses

• Used to study relationship between skills in science simulation

  ( M. S. Pedro et al. (2014))

• Used to study which research skills help graduate students learn other research skills, across several years (Kang et al. (2022))

Specifically, if you master skill A are you starting off better in skill B. Kang and her colleagues used it to study which research skills help graduate students learn other research skills across several years. In that case every year the grad student might be getting better in each of several research skills, and the question is if they acquire skill A in year N are they better at skill B in your N plus one?

Uses

• Contextualization approaches do not appear to lead to overall improvement on predicting within-tutor performance

• But they can be useful for other purposes

  • Predicting robust learning

  • Understanding learning better

  • Understanding relationships between skills

Overall, across all four of these types of examples, contextualization approaches generally don’t appear to lead to big overall improvements in predicting xatutor performance (see Gonzales-Brenes et al., 2014). But in general, they’re really good for other purposes, like predicting robust learning, understanding learning better, and understanding the relationship between the skills.

There are a lot of utilities to modifying the assumptions of BKT that are harder with some of the more contemporary algorithms which is one of the reasons why researchers still sometimes use BKT.

Thank you!

References

Almeda, Ma Victoria, and Ryan S Baker. 2020. “Predicting Student Participation in STEM Careers: The Role of Affect and Engagement During Middle School.” Journal of Educational Data Mining 12 (2): 33–47.

Baker, Ryan S, Sujith M Gowda, and Eyad Salamin. 2018. “Modeling the Learning That Takes Place Between Online Assessments.” In Proceedings of the 26th International Conference on Computers in Education, 21–28.

Baker, Ryan S, Arnon Hershkovitz, Lisa M Rossi, Adam B Goldstein, and Sujith M Gowda. 2013. “Predicting Robust Learning with the Visual Form of the Moment-by-Moment Learning Curve.” Journal of the Learning Sciences 22 (4): 639–66.

Baker, Ryan SJ d, Albert T Corbett, and Vincent Aleven. 2008. “More Accurate Student Modeling Through Contextual Estimation of Slip and Guess Probabilities in Bayesian Knowledge Tracing.” In Intelligent Tutoring Systems: 9th International Conference, ITS 2008, Montreal, Canada, June 23-27, 2008 Proceedings 9, 406–15. Springer.

Baker, Ryan SJ d, Albert T Corbett, Ido Roll, and Kenneth R Koedinger. 2008. “Developing a Generalizable Detector of When Students Game the System.” User Modeling and User-Adapted Interaction 18: 287–314.

Baker, Ryan SJd. 2007. “Modeling and Understanding Students’ Off-Task Behavior in Intelligent Tutoring Systems.” In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, 1059–68.

Baker, Ryan SJD, Adam B Goldstein, and Neil T Heffernan. 2011. “Detecting Learning Moment-by-Moment.” International Journal of Artificial Intelligence in Education 21 (1-2): 5–25.

Beck, Joseph E, Kai-min Chang, Jack Mostow, and Albert Corbett. 2008. “Does Help Help? Introducing the Bayesian Evaluation and Assessment Methodology.” In Intelligent Tutoring Systems: 9th International Conference, ITS 2008, Montreal, Canada, June 23-27, 2008 Proceedings 9, 383–94. Springer.

Corbett, Albert T., and John R. Anderson. 1995. “Knowledge Tracing: Modelling the Acquisition of Procedural Knowledge.” User Model. User Adapt. Interact. 4 (4): 253–78. https://doi.org/10.1007/BF01099821.

De Sande, Brett van. 2013. “Properties of the Bayesian Knowledge Tracing Model.” Journal of Educational Data Mining 5 (2): 1–10.

Hershkovitz, Arnon, Ryan Baker, Sujith M Gowda, and Albert T Corbett. 2013. “Predicting Future Learning Better Using Quantitative Analysis of Moment-by-Moment Learning.” In Educational Data Mining 2013.

Jiang, Yang, Ryan S Baker, Luc Paquette, Maria San Pedro, and Neil T Heffernan. 2015. “Learning, Moment-by-Moment and over the Long Term.” In Artificial Intelligence in Education: 17th International Conference, AIED 2015, Madrid, Spain, June 22-26, 2015. Proceedings 17, 654–57. Springer.

Kang, Jina, Ryan Baker, Zhang Feng, Chungsoo Na, Peter Granville, and David F Feldon. 2022. “Detecting Threshold Concepts Through Bayesian Knowledge Tracing: Examining Research Skill Development in Biological Sciences at the Doctoral Level.” Instructional Science 50 (3): 475–97.

Moore, Gregory R, Ryan Shaun Baker, and Sujith M Gowda. 2015. “The Antecedents of Moments of Learning.” In CogSci.

Pardos, Zachary A, Ryan SJD Baker, Maria OCZ San Pedro, Sujith M Gowda, and Supreeth M Gowda. 2014. “Affective States and State Tests: Investigating How Affect and Engagement During the School Year Predict End-of-Year Learning Outcomes.” Journal of Learning Analytics 1 (1): 107–28.

Pardos, Zachary A, and Michael V Yudelson. 2013. “Towards Moment of Learning Accuracy.” In AIED 2013 Workshops Proceedings Volume, 4:3. Citeseer.

Pedro, Maria Ofelia, Ryan Baker, Alex Bowers, and Neil Heffernan. 2013. “Predicting College Enrollment from Student Interaction with an Intelligent Tutoring System in Middle School.” In Educational Data Mining 2013.

Pedro, Michael Sao, Yang Jiang, Luc Paquette, Ryan S Baker, and Janice Gobert. 2014. “Identifying Transfer of Inquiry Skills Across Physical Science Simulations Using Educational Data Mining.” In. Boulder, CO: International Society of the Learning Sciences.

Slater, Stefan, and Ryan S Baker. 2018. “Degree of Error in Bayesian Knowledge Tracing Estimates from Differences in Sample Sizes.” Behaviormetrika 45 (2): 475–93.

Slater, Stefan, Ryan Baker, Jaclyn Ocumpaugh, Paul Inventado, Peter Scupelli, and Neil Heffernan. 2016. “Semantic Features of Math Problems: Relationships to Student Learning and Engagement.” International Educational Data Mining Society.